

But this picture collapses once you have several particles. That’s an idea to banish from your head straight away! In our particle in a box example, the solutions to Schrödinger’s equation,įor do indeed describe waves along which the particle "goo" might conceivably be spread out. So perhaps the wave function describes a physical wave in space along which the particle is spread out like goo - we never see this particle goo because somehow it contracts to one point when we make a measurement. "There is a sense in which the particle is in all these different places at once, but the worry about saying this is that there still is only one particle," says Short. Most physicists believe that experiments like the double slit experiment suggest that a particle really can become delocalised in space. It was later developed by David Bohm and has become known as the pilotwave or causal interpretation of quantum mechanics, or as Bohmian mechanics. De Broglie did indeed pioneer such a deterministic approach. So perhaps the probabilities given by the wave function measure our ignorance in a similar way: as the particle is moving around in a box, say, it's somewhere definite all the time, only we just can't tell where until we make a measurement. We normally use probabilities to quantify our ignorance: if I say a coin has a fifty-fifty chance of coming up heads or tails, then this simply reflects the fact that I don't yet know how it will come up after the next throw. Unlike a classical description of a physical system, the wave function does not give us definite information about the location of a particle at a given time t - it only gives us the probability of finding the particle in a given location at time t.
Schrodinger equation explained how to#
The next question is how to interpret the wave function. (We say "usually" here because this general argument does not always apply: there are situations in which quantum effects do become perceptible at a macroscopic scale.) A wave is not a wave So small that we usually don't perceive the waviness of macroscopic objects. But Planck's constant is so incredibly small, that even the tiniest bit of mass and velocity make the wavelength vanishingly small as well. One consequence of quantum mechanics is that no object is ever completely at rest, so will never be zero. (Again see the first article of this series.) The momentum of an object is its mass times its velocity. One question that comes up immediately is why we never see big objects like tables, chairs, or ourselves behave like waves.Īs a heuristic argument, recall de Broglie’s relationship between the wavelength and the momentum of a "matter wave": So what, exactly, does quantum mechanics tell us about physical reality? Schrödinger's equation grew out of the idea that particles such as electrons behave like particles in some situations and like waves in others: that's the so-called wave-particle duality (see the first article of this series).
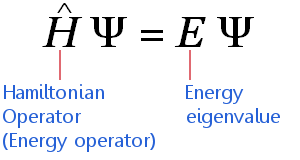
For example, with our particle in a box gives the probability density for finding the particle at position But it is also possible to solve Schrödinger’s equation for many particle systems and to find wave functions for other observable quantities, for example the momenta of the particles. In quantum mechanics the information about the system is contained in the solution to Schrödinger’s equation, a wave function The square of the absolute value of the wave function, is interpreted as a probability density.
Schrodinger equation explained full#
In classical mechanics what you’re after are the positions and momenta of all particles at every time : that gives you a full description of the system. Schrödinger’s equation is to quantum mechanics what Newton’s second law of motion is to classical mechanics: it describes how a physical system, say a bunch of particles subject to certain forces, will change over time.


 0 kommentar(er)
0 kommentar(er)
